视图变换

相机

相机的位置\(\overrightarrow{e}\)

相机的视线\(\widehat{g}\)

相机向上方向\(\widehat{t}\)

视图变换

将所有物品和相机进行移动，使得相机移动到标准位：相机处于原点，向-Z方向看，向上方向为Y

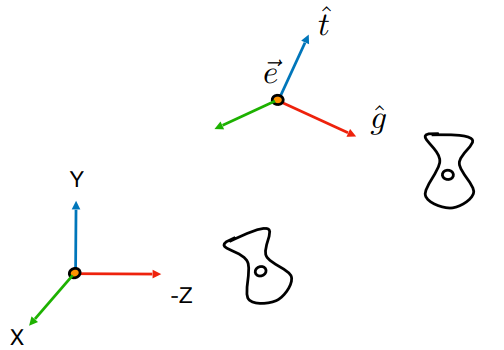
先将 \(\overrightarrow{e}\) 平移到原点，再将 \(\widehat{g}\) 旋转到 -Z 方向，再将 \(\widehat{t}\) 旋转到 Y 方向，最后将 \((g \times t)\) 旋转到 X 方向。

\(M_{\text {view }}=R_{\text {view }} T_{\text {view }}\)

1.平移 \(\overrightarrow{e}\) 到原点
\(
T_{\text {view }}=\begin{bmatrix}
1 & 0 & 0 & -x_e \\
0 & 1 & 0 & -y_e \\
0 & 0 & 1 & -z_e \\
0 & 0 & 0 & 1
\end{bmatrix}
\)

2. 旋转 \(\widehat{g}\) 到 -Z 方向，旋转 \(\widehat{t}\) 到 Y 方向，旋转 \((g \times t)\) 到 X 方向。
\(
R_{\text {view }}=
\begin{bmatrix}
x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\
x_t & y_t & z_t & 0 \\
x_{-g} & y_{-g} & z_{-g} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\)

投影

投影分为正交投影和透视投影

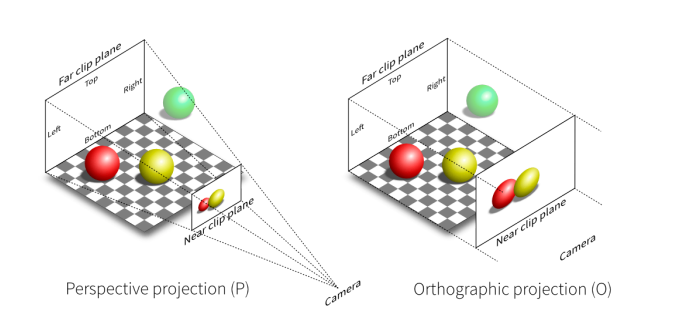
视景体

视景体是指由摄像机或观察者所看到的场景的几何形状，它是由6个平面确定的区域，这6个平面分别为上平面（up）、下平面（down）、左平面（left）、右平面（right）、远平面（far）和近平面（near）。视景体内的物体可以被投影到近平面上，而视景体外面的物体则会被裁剪掉。

l（left）：视景体左侧相对于相机的距离。
r（right）：视景体右侧相对于相机的距离。
n（near）：视景体近端相对于相机的距离。
f（far）：视景体远端相对于相机的距离。
t（top）：视景体上侧相对于相机的距离。
b（bottom）：视景体下侧相对于相机的距离。

正交投影

1.定义一个立方体，即视景体\([l,r]\times[b,t]\times[f,n]\)
2.将视景体的中心移动到原点
3.将视景体的边长拉升成\([-1,1]^3\)
4.得到一个Canonical（正则、规范、标准）立方体

判断远近：使用原立方体的z坐标 \([f,n]\)，由于是看向-Z方向，所以当Z坐标值越大，离相机越近，Z坐标值越小，离相机越远

数学表达：
先将中心平移到原点上，然后进行缩放
\(
M_{\text {ortho }}=
\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{bmatrix}
\)

但由于有之前的视图变换，视景体n、f平面的中心就在Z轴上，所以平移时只需要将视景体沿Z轴平移使中心在坐标原点上。
并且有\(r=-l\)，\(b=-t\)。
所以公式可以进行简化
\(
M_{\text {ortho }}=
\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{bmatrix}
\)

透视投影

根据齐次坐标的定义 \(
\begin{bmatrix}
x / w \\
y / w \\
z / w \\
1
\end{bmatrix}, w \neq 0
\) 可知，将里面每个元素乘以\(k(k\ne 0)\)后，表示的是同一向量。

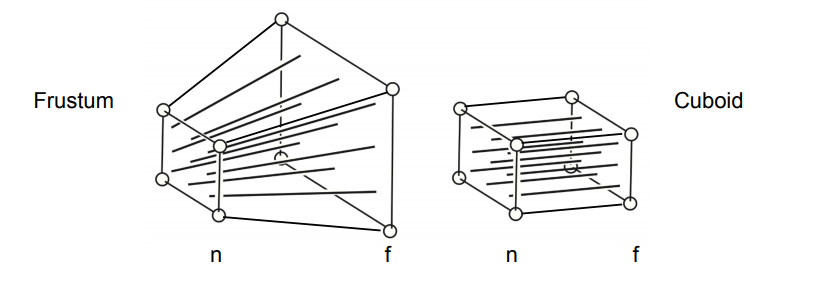
在进行透视投影时，先将透视投影的棱台进行挤压，直到变成视景体，即一个长方体，然后再进行正交投影

在挤压时，要遵循：
1.近平面挤压后不变
2.远平面挤压后Z值不变
3.远平面的中心挤压后仍然为中心

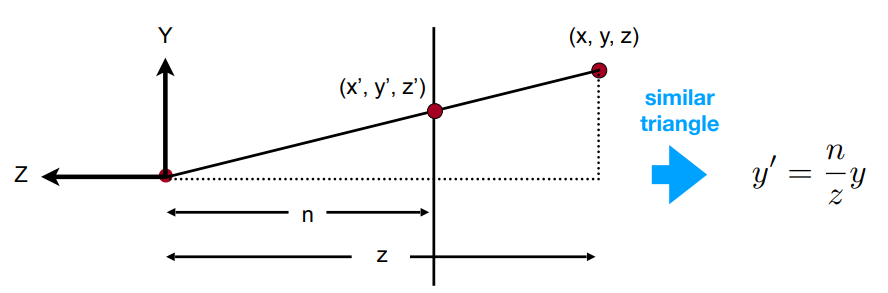
对于点\((x,y,z)\)被挤压后得到\((x^{\prime},y^{\prime}, z^{\prime})\) ，根据相似三角形可得：
\(x^{\prime}=\frac{n}{z} x\)
\(y^{\prime}=\frac{n}{z} y\)

写作齐次坐标为：
\(
\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}
\Rightarrow
\begin{bmatrix}
n x / z \\
n y / z \\
\text { unknown } \\
1
\end{bmatrix}
\stackrel{\text { mult. by z }}{==}
\begin{bmatrix}
n x \\
n y \\
\text { still unknown } \\
z
\end{bmatrix}
\)

于是可以得出\(M_{\text {persp } \rightarrow \text { ortho }}\)为：
\(
M_{\text {persp } \rightarrow \text { ortho }}=
\begin{bmatrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{bmatrix}
\)

现在需要求出Z坐标，也就是上述矩阵的第三行。

根据以上压缩时遵循的三个原则的第一点，近平面挤压后不变，可以写出以下方程
\(
\begin{bmatrix}
x \\
y \\
n \\
1
\end{bmatrix}\Rightarrow\begin{bmatrix}
x \\
y \\
n \\
1
\end{bmatrix}==\begin{bmatrix}
n x \\
n y \\
n^2 \\
n
\end{bmatrix}
\)

因此，第三行的形式为\(\begin{bmatrix}0 &0 &A &B\end{bmatrix}\)
\(
\begin{bmatrix}0 &0 &A &B\end{bmatrix}
\begin{bmatrix}0\\ 0\\ A\\ B\end{bmatrix}
=n^2
\)

即\(A n+B=n^2\)

根据以上原则的第二点，远平面挤压后Z值不变，可以写出以下方程
\(
\begin{bmatrix}
0 \\
0 \\
f \\
1
\end{bmatrix}\Rightarrow\begin{bmatrix}
0 \\
0 \\
f \\
1
\end{bmatrix}==\begin{bmatrix}
0 \\
0 \\
f^2 \\
f
\end{bmatrix}
\)

即\(A f+B=f^2\)

联立2个方程，可以解出A、B
\(
\begin{aligned}
& A=n+f \\
& B=-n f
\end{aligned}
\)

综上，可以得出\(M_{\text {persp } \rightarrow \text { ortho }}\)为：
\(
M_{\text {persp } \rightarrow \text { ortho }}=
\begin{bmatrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{bmatrix}
\)