向量

向量长度：\(\left | \overrightarrow{a} \right |\)

单位向量：\(\widehat{a}= \frac{\overrightarrow{a}}{\left | \overrightarrow{a} \right | }\)

\(A=\begin{bmatrix}x\\y\end{bmatrix}\)

\(A^{T} =\begin{bmatrix}x&y\end{bmatrix}\)

\(\left | A \right | =\sqrt{x^2+y^2}\)

向量的乘法

点乘

运算

\(\overrightarrow{a}\cdot \overrightarrow{b}=\left | \overrightarrow{a} \right | \left | \overrightarrow{b} \right | cos\theta\)

\(cos\theta =\frac{ \overrightarrow{a}\cdot \overrightarrow{b}}{\left | \overrightarrow{a} \right | \left | \overrightarrow{b} \right | }\)

对于单位向量：\(cos\theta =\widehat{a}\cdot\widehat{b}\)

\( \overrightarrow{a}\cdot \overrightarrow{b} = \overrightarrow{b}\cdot \overrightarrow{a} \)

\(\overrightarrow{a}\cdot \left ( \overrightarrow{b}+\overrightarrow{c}\right ) =\overrightarrow{a}\cdot\overrightarrow{b}+\overrightarrow{a}\cdot\overrightarrow{c}\)

\(\left ( k\overrightarrow{a}\right )\cdot \overrightarrow{b} =\overrightarrow{a}\cdot \left ( k\overrightarrow{b}\right )=k\left (\overrightarrow{a}\cdot \overrightarrow{b}\right )\)

In 2D：\(\overrightarrow{a}\cdot \overrightarrow{b}=\begin{bmatrix}x_{a} \\y_{a}\end{bmatrix}\cdot \begin{bmatrix}x_{b} \\y_{b}\end{bmatrix}=x_{a}x_{b}+y_{a}y_{b}\)

In 3D：\(\overrightarrow{a}\cdot \overrightarrow{b}=\begin{bmatrix}x_{a} \\y_{a}\\z_{a}\end{bmatrix}\cdot \begin{bmatrix}x_{b} \\y_{b}\\z_{b}\end{bmatrix}=x_{a}x_{b}+y_{a}y_{b}+z_{a}z_{b}\)

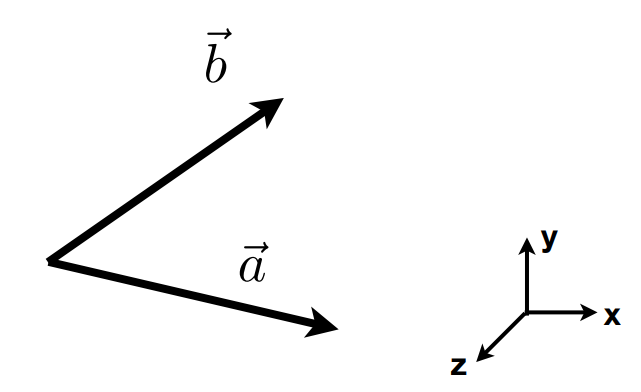
投影

\(\overrightarrow {b}_{\bot}\)：b到a的投影

\(\overrightarrow {b}_{\bot}\) 必须沿着\(\overrightarrow{a} \)或 \(\widehat{a} \)

即 \(\overrightarrow {b}_{\bot}=k\widehat{a} \)

\(k=\left | \overrightarrow {b}_{\bot} \right | = \left | \overrightarrow {b} \right | cos\theta \)

点乘在图形学中的应用

求两个向量之间的角度，例如光源和表面之间角度的余弦。

寻找一个向量在另一个向量上的投影。

计算两个向量有多近。

分解向量：
沿 \(\overrightarrow{a} \) 方向 \(\overrightarrow {b}_{\bot}\)
和垂直于 \(\overrightarrow{a} \) 方向： \( \overrightarrow {b} -\overrightarrow {b}_{\bot}\)

确定向量方向：
点乘结果>0同向
<0反向
=0垂直

叉乘

叉乘的运算

叉积与两个初始向量正交

右手螺旋定则决定方向

\(\left |a \times b\right |=\left|a\right| \left|b\right| \sin \phi\)

\(\vec{x} \times \vec{y}=+\vec{z}\)
\(\vec{y} \times \vec{x}=-\vec{z}\)
\(\vec{y} \times \vec{z}=+\vec{x}\)
\(\vec{z} \times \vec{y}=-\vec{x}\)
\(\vec{z} \times \vec{x}=+\vec{y}\)
\(\vec{x} \times \vec{z}=-\vec{y}\)

\(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)
\(\vec{a} \times \vec{a}=\overrightarrow{0}\)
\(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)
\(\vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b})\)

\(\vec{a} \times \vec{b}=\begin{bmatrix}
y_a z_b-y_b z_a \\
z_a x_b-x_a z_b \\
x_a y_b-y_a x_b
\end{bmatrix}\)

\(\vec{a} \times \vec{b}=A^* b=\begin{bmatrix}
0 & -z_a & y_a \\
z_a & 0 & -x_a \\
-y_a & x_a & 0
\end{bmatrix}\begin{bmatrix}
x_b \\
y_b \\
z_b
\end{bmatrix}\)

点乘在图形学中的应用

确定左/右

叉积为正在左边，叉积为负在右边

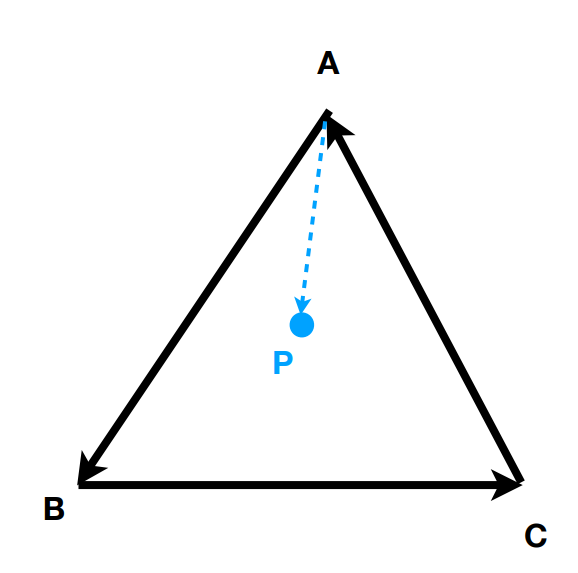
确定内部/外部

叉积结果全为正或负则在三角形内部，否则在外部

正交坐标系

\(\left|\vec{u}\right|=\left|\vec{v}\right|=\left|\vec{w}\right|=1\)
\( \vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0 \)
\(\vec{w}=\vec{u} \times \vec{v} \quad\)
\(\vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w}\)（投影）

矩阵

矩阵的乘法

矩阵A的列数必须等于矩阵B的行数
(M x N) (N x P) = (M x P)

积中的元素(i, j)为A中的第i行和B中的第j列的点积

\(\begin{bmatrix}
1 & 3 \\
5 & 2 \\
0 & 4
\end{bmatrix}\begin{bmatrix}
3 & 6 & 9 & 4 \\
2 & 7 & 8 & 3
\end{bmatrix}=\begin{bmatrix}
9 & 27 & 33 & 13 \\
19 & 44 & 61 & 26 \\
8 & 28 & 32 & 12
\end{bmatrix}\)

运算法则

没有交换律

结合律和分配律：
(AB)C=A(BC)
A(B+C) = AB + AC
(A+B)C = AC + BC

矩阵的转置

交换行和列(ij -> ji)

\(\begin{bmatrix}
1 & 2 \\
3 & 4 \\
5 & 6
\end{bmatrix}^T=\begin{bmatrix}
1 & 3 & 5 \\
2 & 4 & 6
\end{bmatrix}\)

运算律

\((A B)^T=B^T A^T\)

单位矩阵

\(I_{3 \times 3}=\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}\)

\(A A^{-1}=A^{-1} A=I\)

\((A B)^{-1}=B^{-1} A^{-1}\)

矩阵形式的向量乘法

\(\begin{aligned}
& \vec{a} \cdot \vec{b}=\vec{a}^T \vec{b} \\
= & \begin{bmatrix}
x_a & y_a & z_a
\end{bmatrix}\begin{bmatrix}
x_b \\
y_b \\
z_b
\end{bmatrix}=\left(x_a x_b+y_a y_b+z_a z_b\right)
\end{aligned}\)

\(\vec{a} \times \vec{b}=A^* b=\begin{bmatrix}
0 & -z_a & y_a \\
z_a & 0 & -x_a \\
-y_a & x_a & 0
\end{bmatrix}\begin{bmatrix}
x_b \\
y_b \\
z_b
\end{bmatrix}\)